Memory for Generative Art

My algorithms for generative art are far from deterministic. In each execution, a flurry of decisions is made about how the piece should be generated. Decisions within the algorithm are usually constrained with bounds to introduce consistency between the pieces. Bounds of varying sizes can lead to a vast number of possibilities, making executions difficult to reproduce.

Repeatable executions reduce the rarity of the pieces, but they also come with significant benefits. For example, uniqueness can be enforced by avoiding repetition, and constraints on the algorithm can be fine-tuned based on previous results. To accomplish this, decisions made during execution must be traced and codified into a reversible format. By reversing the format into the original decisions, the execution of the algorithm can be repeated.

Tracing Decisions

For the purpose of this exploration, a decision is a split point in the execution flow of a program. Decisions can manifest in a variety of ways, such as conditional statements or results of computed variables. Due to the complexities around what can be considered a decision, it is up to the code author to determine what decisions are relevant. This open-ended approach may also reveal new use cases and applications of the solution.

There are two dimensions to tracing decisions: the order in which they occur and the data they produce. Both dimensions can be captured in a data structure that stores values while preserving connections with direction.

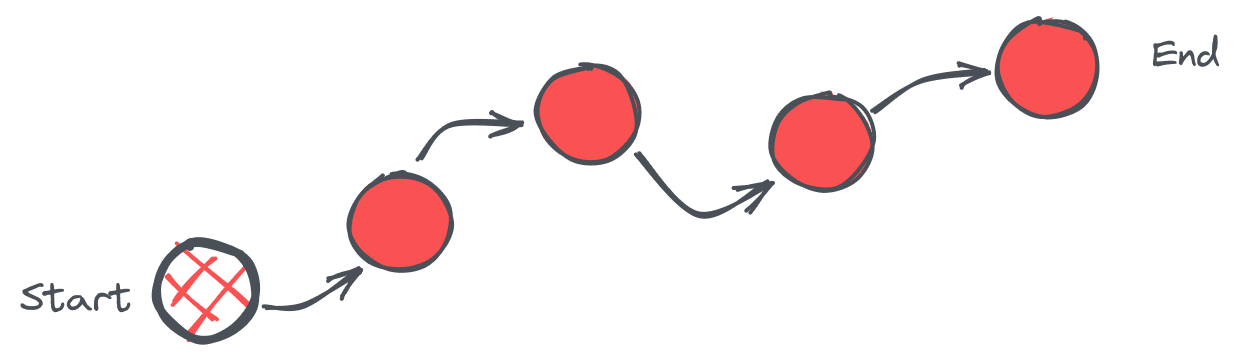
The initial candidates with these properties were the linked list and graph structures. I could argue that a linked list is a special kind of graph, but I could be wrong. Both structures use nodes to hold data and edges (or links) to describe the relationship between the data. Data stored in these nodes could also be complex, making the structures even more descriptive.

Retrieving data would typically be performed by searching for a particular decision or the sequence of decisions. In both structures, traversing the nodes will accomplish retrieval and, in the worst cases, require you to check every node.

Maintaining Order

In the illustration above, all nodes can only possess one edge. This edge points to the next node in the structure. If there are no remaining nodes, then it points to nothing. An advantage of this approach is that the order is directed and reflected in the structure itself, and operations are simpler with only one way to repeat the order. More complex scenarios could require more than one edge between nodes.

For example, having two edges unlocks the ability to traverse the structure in either direction. Traversals in any direction also permit using any node as the starting node for some operation. More creative algorithms might even traverse in both directions, maybe to find a value. With generative art, this could be used to step through an execution, supporting forward and backward controls.

Altering the number of edges allowed within the structure can drastically change the operations performed on it. More complex relationships can be derived, such as networks and patterns that emerge within the structure.

Decision Trees

An advantage of graphs is that, for the most part, they merge well with similar graphs. This property can be leveraged to create a unified graph by merging existing single-edged graphs. Nodes found at the same location in two incoming graphs will be merged into one. This unified graph can be used to store all previous decisions.

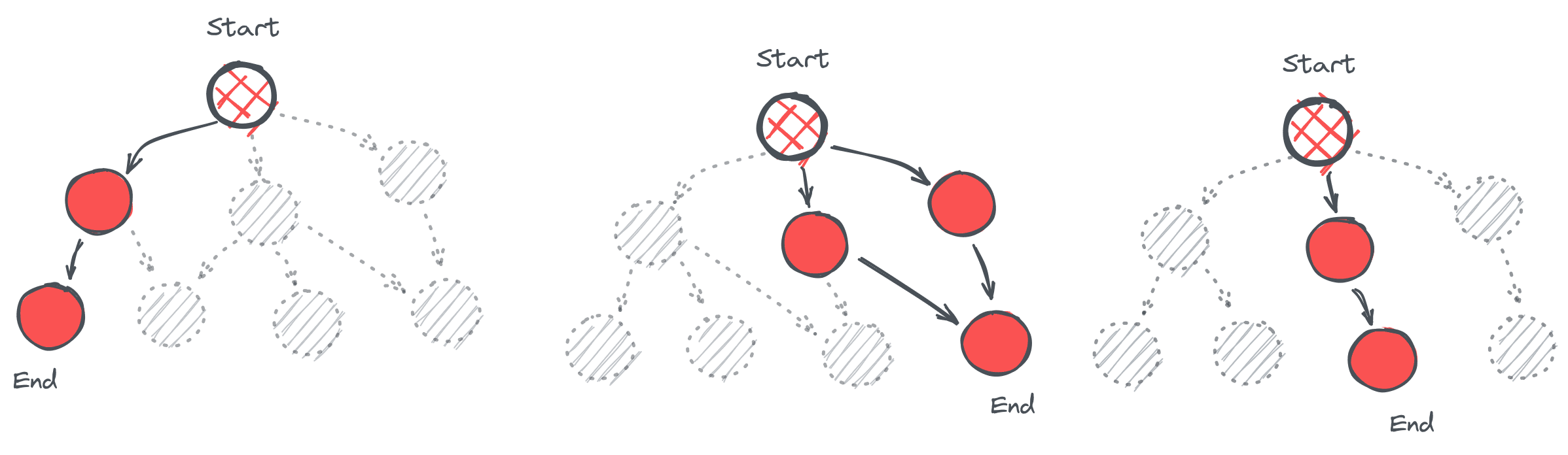
Access to all previous decisions can provide a path to enforcing uniqueness and identifying common and rare paths.

Continuing on

There may be many more viable solutions to this problem, and it's exciting to continue discovering them. Taking benchmarks will be required to compare solutions, which will likely become the next focus for the next little while.